Homework 4: Preference Optimization
Start on Nov 3 | Due on Nov 17 With grace days Nov 19
Getting Started
If you have already cloned my homework repository nlp-class-hw for
previous homeworks then go into that directory and update the directory:
git pull origin/master
cd nlp-class-hw/prefopt
If you don’t have that directory anymore then simply clone the repository again:
git clone https://github.com/anoopsarkar/nlp-class-hw.git
Clone your own repository from GitLab if you haven’t done it already:
git clone git@github.sfu.ca:USER/nlpclass-1257-g-GROUP.git
Note that the USER above is the SFU username of the person in
your group that set up the GitLab repository.
Then copy over the contents of the prefopt directory into your
hw3 directory in your repository.
Set up the virtual environment:
python3.10 -m venv venv
source venv/bin/activate
pip3 install -r requirements.txt
You must use Python 3.10 (or later) for this homework.
Note that if you do not change the requirements then after you have
set up the virtual environment venv you can simply run the following
command to get started with your development for the homework:
source venv/bin/activate
Background
The goal for this homework is to convert a large language model (LLM) that is good at the next token prediction task to follow instructions and be a helpful assistant.
We are going to change the language model parameters using preference optimization in order to make the LM follow instructions. This process is often called “instruct tuning”.
In order to instruct tune an LLM we will be using a dataset of prompts related to a variety of tasks, along with constraints on what is the preferred output format. The preferred output is also provided in the dataset. What is missing from the dataset is the dispreferred output, which is assumed to be what the LLM produces before instruction tuning.
Here is an example of an instruction prompt for an LLM assistant and a constraint on the output:
prompt
You will be given a piece of text either about an everyday event,
or a general statement. If the event seems impossible for you, or
the general statement does not make sense matches your commonsense,
output 'False', otherwise output 'True'.
Text: It was raining so hard that the water in the ocean boiled.
constraints
The output should be one of the two: 'True' or 'False'.
The reference output is also provided:
output
False
This is just one example. To train the LLM to follow instructions requires tens of thousands of examples.
The goal is to use training data of this type in order to improve the accuracy of the LLM.
Note that LLM output that is incorrect or does not follow the instructions in the prompt is not provided in this dataset.
Data set
The data set for this homework is called Unnatural Instructions which is a medium sized dataset curated specifically for instruction tuning.
The data and the various tasks are described in detail in the following publication:
Unnatural Instructions: Tuning Language Models with (Almost) No Human Labor. Or Honovich, Thomas Scialom, Omer Levy, Timo Schick.
The dataset has 68K examples with each example having three strings stored as JSON data:
- Prompt
- Constraint
- Output
Note that newline escapes are used because the strings are stored in the JSON format.
Data files
The data files provided are:
data/train.txt.gz– the inputs in the training data including prompt and constraint.data/train.out.gz– the expected answer for each prompt intrain.txt.data/input– input filesdev.txtandtest.txt.data/reference/dev.out– the reference output for thedev.txtinput file.data/train_default.out.gz– useful data but not strictly required.
The Model
We will be using the Qwen/Qwen2.5-0.5B-Instruct model for this
homework. You cannot use any other LLM as a substitute.
Qwen2.5 is a family of base language models and instruction-tuned language models ranging from 0.5 to 72 billion parameters. We will be using the 0.5B parameter model to reduce compute demands.
Default solution
The default solution is provided in answer/default.py. To use the default
as your solution:
cd answer
cp default.py prefopt.py
cp default.ipynb prefopt.ipynb
cd ..
python3 zipout.py
python3 check.py
The default solution uses the LLM specified above to take input prompts and constraints and produce outputs that attempt to provide a helpful answer.
Please do not commit your tune model file or the original language model file into your git repository as it is very large and you will go over your disk quota.
To run the default program as follows:
python answer/default.py -i data/input/dev.txt -d cuda:0 -l log.txt > output.txt
You might see a warning You seem to be using the pipelines sequentially on GPU.. You can ignore this warning.
And then you can check the score on the dev output file called output.txt by running:
python output_check.py -t data/reference/dev.out -o output.txt
which produces the evaluation score
Score=29.0000
Make sure that the command line options are kept as they are in
answer/default.py. You can add to them but you must not delete any
command line options that exist in answer/default.py.
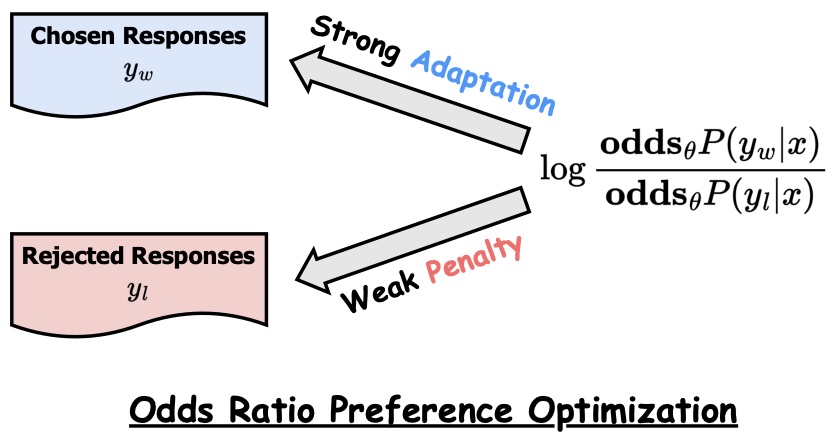
Preference Optimization for Instruct Tuning
You will implement the approach presented in this paper which is a direct preference optimization approach to instruct tuning:
ORPO: Monolithic Preference Optimization without Reference Mode. Jiwoo Hong, Noah Lee, and James Thorne.
Instead of implementing this from scratch we will use an existing implementation. There are a few implementations out there but the Huggingface TRL library contains an implementation of ORPO that is easy to use.
Here are some useful links to get you started on implementing ORPO for this homework:
- ORPO trainer in TRL
- ORPO trainer TRL source code
- Training arguments in HFargumentparser
- Hyperparameter settings for ORPO
- Original Github repo for ORPO
Training an ORPO model using TRL requires data in the following format:
orpo_dataset_dict = {
"prompt": [
"hello",
"hello",
"how are you",
"What is your name?",
"What is your name",
"Which is the best programming language?",
"Which is the best programming language?",
"Which is the best programming language?",
],
"chosen": [
"hi, nice to meet you.",
"hi nice to meet you",
"I am fine",
"My name is Qwen.",
"My name is Qwen",
"My name is Qwen",
"Python",
"Python 3",
"Java",
],
"rejected": [
"leave me alone",
"Sent from my iPhone",
"I am not fine",
"Whats it to you?",
"I dont have a name",
"My name is Claude",
"Javascript",
"Fortran",
"C++",
],
}
Once you have a dataset in this format, you can load it using the datasets library from Huggingface:
from datasets import Dataset
full_dataset = Dataset.from_dict(orpo_dataset_dict)
dataset = full_dataset.train_test_split(test_size=0.05)
Using the HFArgumentParser makes it easy to get the hyperparameters into your training script:
parser = HfArgumentParser((ScriptArguments, ORPOConfig, ModelConfig))
script_args, training_args, model_config = parser.parse_args_into_dataclasses()
Using TRL for training using ORPO is easy and similar to using the peft library:
orpo_trainer = ORPOTrainer(
model,
args=training_args,
train_dataset=dataset["train"],
eval_dataset=dataset["test"] if training_args.eval_strategy != "no" else None,
processing_class=tokenizer,
peft_config=get_peft_config(model_config),
)
orpo_trainer.train()
orpo_trainer.save_model(training_args.output_dir)
Pay careful attention to the hyperparameters as training takes quite a bit of compute even with a GPU. You can use parameter efficient fine-tuning method like LORA or fully instruct tune the model. LORA will be more compute efficient with some minor penalty in performance.
Here are some hyperparameters to get you started. You do not have to do extensive grid search on these to improve performance:
python orpo.py \
--per_device_train_batch_size 4 \
--max_steps 1000 \
--learning_rate 8e-5 \
--gradient_accumulation_steps 1 \
--logging_steps 10 \
--eval_steps 500 \
--output_dir="qwen2.5-0.5B-Instruct-lora-aligned-orpo" \
--optim rmsprop \
--warmup_steps 150 \
--bf16 \
--logging_first_step \
--no_remove_unused_columns \
--use_peft \
--lora_r=16 \
--lora_alpha=24
Discussion on the forum in Coursys is encouraged!
Required files
You must create the following files:
answer/prefopt.py– this is your solution to the homework. start by copyingdefault.pyas explained below.answer/prefopt.ipynb– this is the iPython notebook that will be your write-up for the homework.
Run your solution on the data files
To create the output.zip file for upload to Coursys do:
python3 zipout.py
For more options:
python3 zipout.py -h
Check your accuracy
To check your accuracy on the dev set:
python3 check.py
The output score is found using the check.py script:
python3 check.py -h
In particular use the log file to check your output evaluation:
python3 check.py -l log
The accuracy on data/input/test.txt will not be shown. We will
evaluate your output on the test input after the submission deadline.
Submit your homework on Coursys
Once you are done with your homework submit all the relevant materials to Coursys for evaluation.
Create output.zip
Once you have a working solution in answer/prefopt.py create
the output.zip for upload to Coursys using:
python3 zipout.py
Create source.zip
To create the source.zip file for upload to Coursys do:
python3 zipsrc.py
You must have the following files or zipsrc.py will complain about it:
answer/prefopt.py– this is your solution to the homework. start by copyingdefault.pyas explained below.answer/prefopt.ipynb– this is the iPython notebook that will be your write-up for the homework.
Each group member should write about what they did for this homework in the Python notebook.
Upload to Coursys
Go to Homework 4 on Coursys and do a group submission:
- Upload
output.zipandsource.zip - Make sure you have documented your approach in
answer/prefopt.ipynb. - Make sure each member of your group has documented their contribution to this homework in the Python notebook.
Grading
The grading is split up into the following components:
- dev scores (see Table below)
- test scores (see Table below)
- iPython notebook write-up
- Make sure that you are not using any external data sources in your solution.
- Make sure you have implemented the fine-tuning model improvements yourself without using external libraries.
- Check if each group member has written about what they did in the Python notebook.
Your score should be equal to or greater than the score listed for the corresponding marks.
| Score(dev) | Score(test) | Marks | Grade |
| 0.0 | 0.0 | 0 | F |
| 18 | 22 | 55 | D |
| 28 | 32 | 60 | C- |
| 29 | 33 | 65 | C |
| 30 | 34 | 70 | C+ |
| 31 | 35 | 75 | B- |
| 32 | 36 | 80 | B |
| 33 | 37 | 85 | B+ |
| 34 | 38 | 90 | A- |
| 35 | 39 | 95 | A |
| 52 | 46 | 100 | A+ |
The score will be normalized to the marks on Coursys for the dev and test scores.